இந்திய முறைப்படி கடவுள் வணக்கத்தில்தான் ஆர்யபடர் தொடங்குகிறார். பிரமன், பூமி, சந்திரன், புதன், வெள்ளி, சூரியன், செவ்வாய், வியாழன், சனி, நட்சத்திரங்கள் ஆகியவற்றுக்கு முறையே வணக்கத்தைத் தெரிவித்துவிட்டு, குசுமபுரத்தில் மதிக்கப்படும் ஞானத்தை விளக்கத் தொடங்குகிறார்.
பிற கணித ஆசிரியர்கள், சிவன், விஷ்ணு அல்லது மகாவீரரை வணங்கித் தொழுது ஆரம்பிக்கையில் ஆர்யபடர், பிரமனில் தொடங்கியிருப்பது சுவாரசியம்.
கணிதத்தில் மிகப்பெரும் பாய்ச்சல் என்பது எண்களை Place Value எனப்படும் இடப்பெறுமான முறையில் குறிப்பிடுவது. 15 என்று ஓர் எண்ணை எழுதும்போது அதன் மதிப்பு (5×1 + 1×10) என்று ஆகிறது. இம்மாதிரி, பத்தடிமான முறையில் – ஓர் எண்ணின் அடுத்தடுத்த இலக்கங்கள் பத்தின் மடங்குகளாக உயர்வதாக எண்களைக் கொண்டுவந்ததுதான் இந்தியா உலகுக்கு அளித்த கொடை. இதில் 0 என்ற எண்ணைப் பயன்படுத்தியதுதான் இந்தியாவின் மாபெரும் பாய்ச்சல். 15 என்பது வேறு, 105 என்பது வேறு என்று வேறுபடுத்திக் காட்டியது. இதுகூட ஆர்யபடரின் காலத்துக்கு முன்பே இருந்திருக்கிறது.
சில பாடபுத்தகங்களில் தவறாக ஆர்யபடர்தான் ‘0’வைக் கண்டுபிடித்தார் என்று கூறுவதுண்டு. அதில் எந்த உண்மையும் இல்லை. பிற நாகரிகங்களிலும் 0 என்ற எண் பயன்பாட்டில் இருந்துள்ளது. ஆனால் இடப்பெறுமான முறையில் எண்கள் எழுதப்பட்டு, கூட்டல், கழித்தல், பெருக்கல், வகுத்தல் நடைபெறவில்லை. இப்போது நமக்குக் கிடைத்துள்ள ஆதாரங்களின்படி, இது இந்தியாவில்தான் நடைமுறைக்கு வந்துள்ளது.
ஆர்யபடர், ஆரம்பிப்பதே இந்த இடப்பெறுமானத்துக்குப் பெயர் அளிப்பதிலிருந்துதான். அடுத்தடுத்த பத்து இலக்கங்களுக்கு அவர் அளிக்கும் பெயர்கள் இவை. முதலில் அவர் தரும் வடமொழிப் பெயரையும், அருகில் இன்று தமிழில் நாம் சொல்லும் பெயரையும், அடுத்து எண் வடிவிலும் அதனைத் தருகிறேன்.
ஏக – ஒன்று – 1
தஶ – பத்து – 10
ஶத – நூறு – 100
ஸஹஸ்ர – ஆயிரம் – 1,000
அயுத – பத்தாயிரம் – 10,000
நியுத – லட்சம் – 1,00,000
ப்ரயுத – பத்து லட்சம் – 10,00,000
கோடி – கோடி – 1,00,00,000
அர்புத – பத்து கோடி – 10,00,00,000
வ்ருந்த – நூறு கோடி – 100,00,00,000
ஆர்யபடர், முழு எண்களைப் பொருத்தமட்டில், கூட்டல், கழித்தல், பெருக்கல், வகுத்தல் என ஒன்றைப் பற்றியும் பேசுவதில்லை. அவருடைய நூலைப் படிப்போருக்கு அவை ஏற்கெனவே தெரியும் என்ற ஊகத்தில் நேராக வர்கம் (square), கனம் (cube) ஆகியவற்றை நோக்கிச் சென்றுவிடுகிறார்.
வர்கம் என்பதை அவர் எண்ரீதியிலும் வடிவரீதியிலும் இணைத்தே விளக்குகிறார். வர்கம் என்பது இரண்டு ஒரே எண்களைப் பெருக்குவது என்கிறார். நான்கு பக்கங்கள் ஒரே அளவிலும் மூலைவிட்டங்கள் ஒரே அளவிலும் உள்ள வடிவத்தைச் சதுரம் என்று நாம் அழைக்கிறோம். அதனை ஆர்யபடர் ‘சமசதுரஶ்ர’ என்கிறார். இந்தச் சதுரத்தின் பரப்பளவும் ‘வர்கமே’ என்கிறார். உரையாசிரியர் முதலாம் பாஸ்கரர் (இனி பாஸ்கரர் என்றே அழைப்போம்), வர்கம் என்பதற்கு கரணி, க்ருதி, வர்கணா, யாவகரணா போன்ற பெயர்களையும் வழங்குகிறார்.
ஆக, இந்த ஒரு வரியில் இரண்டு கருத்துகள் முன்வைக்கப்படுகின்றன. ஒன்று, x^2 = (x) (x) என்னும் சமன்பாடு. மற்றது, ஒரு சதுரத்தின் பரப்பளவு, அதன் ஒரு பக்கத்தை வர்கமாக்குவதன்மூலம் கிடைக்கும் என்பது.
அதேபோல, ஒரே எண்ணை மூன்று முறை பெருக்கினால் கிடைப்பது, ‘கனம்’ என்றும் ஒரே அளவை அதன் மூன்று பரிமாணங்களுக்கும் நீட்டித்து பன்னிரண்டு சம விளிம்புகளைக் கொண்ட ஒரு வடிவம் ‘கனம்’ என்றும் ஆர்யபடர் சொல்கிறார்.
இதன்மூலம் x^3 = (x) (x) (x) என்பதுவும், ஒரு ‘கன’ வடிவத்தின் கொள்ளளவு மேலே சொன்ன சமன்பாட்டின்மூலம் வரும் என்பதுவும் குறிப்பிடப்படுகின்றன.
இதுவரையில் புதிதாக நாம் தெரிந்துகொள்ள ஒன்றும் இல்லை. பள்ளிக்கூடத்தில் நாம் கற்றுக்கொள்வதுதான்.
அடுத்து, வர்கமூலம் என்பதை எவ்வாறு கண்டுபிடிப்பது என்பதற்கான வழிமுறையைத் தருகிறார் ஆர்யபடர்.
இப்போது நம் பள்ளிகளில் வர்க எண் ஒன்றின் மூலத்தைக் கண்டுபிடிக்க நாம் ஒரு வழிமுறையைச் சொல்லிக்கொடுக்கிறோம். அதிலிருந்து சற்றே மாறுபட்ட ஒன்றை ஆர்யபடர் தருகிறார். முதலில் பள்ளிக்கூடத்தில் நாம் கற்றுக்கொள்ளும் முறையைப் பார்ப்போம்.
எடுத்துக்காட்டாக, 4489 என்ற எண்ணை எடுத்துக்கொள்வோம். கொடுக்கப்பட்டுள்ள எண்ணை வலதுபுறத்திலிருந்து இரண்டு இரண்டு இலக்கங்களாகப் பிரிக்க ஆரம்பிக்கவேண்டும். இதன் காரணமாக இடக்கோடியில் ஒற்றை இலக்க எண்ணோ இரட்டை இலக்க எண்ணோ மீதமிருக்கலாம். பிறகு இடமிருந்து வலமாக இயங்கவேண்டும். இங்கே இடதுகோடியில் இருப்பது 44. இந்த எண்ணில் அடங்கக்கூடிய வர்க எண்ணை முதலில் ஊகிக்கவேண்டும். 44-இல் 6-ன் வர்கம் அடங்கும். அதை மேல்கோட்டின் மேலும் பக்கவாட்டிலும் எழுதி, பெருக்கி, 44-ன்கீழ் எழுதிக் கழிக்கவேண்டும். மீதம் வருவது 8.
அடுத்து, 8-க்கு அருகில் இரண்டாவதாக மேலே உள்ள 89-ஐக் கீழே இறக்கி அருகே எழுதிக்கொள்ளவேண்டும். அடுத்ததாக, மேலே உள்ள 6-ஐ இரண்டால் பெருக்கி வரும் விடையான 12-ஐ பக்கவாட்டில் வைத்துக்கொள்ளவேண்டும்.
அடுத்து, ஓரிலக்க எண் ஒன்றை ஊகிக்கவேண்டும். இதனை மேலேயும் எழுதிக்கொள்ளவேண்டும்; 12-க்கு அருகிலும் எழுதிக்க்கொள்ளவேண்டும். இவை இரண்டில் பெருக்குத்தொகை 889-ஆக வருகிறதா என்று பார்க்கவேண்டும். அப்படி ஊகிக்கும்போது, ‘7’ என்பது வருகிறது. 7 x 127 = 889. எனவே 4489 என்பதன் வர்கமூலம் 67.
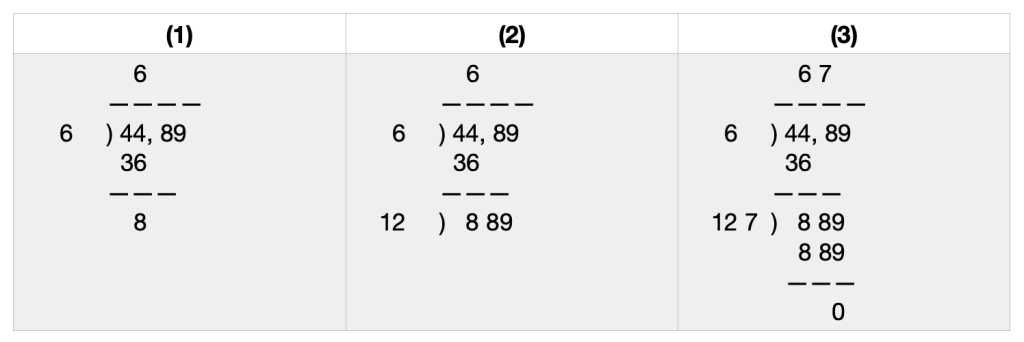
சற்றே பெரிய எண்ணான 59049-ஐ எடுத்துக்கொண்டு இதனைச் செய்துபார்ப்போம்.
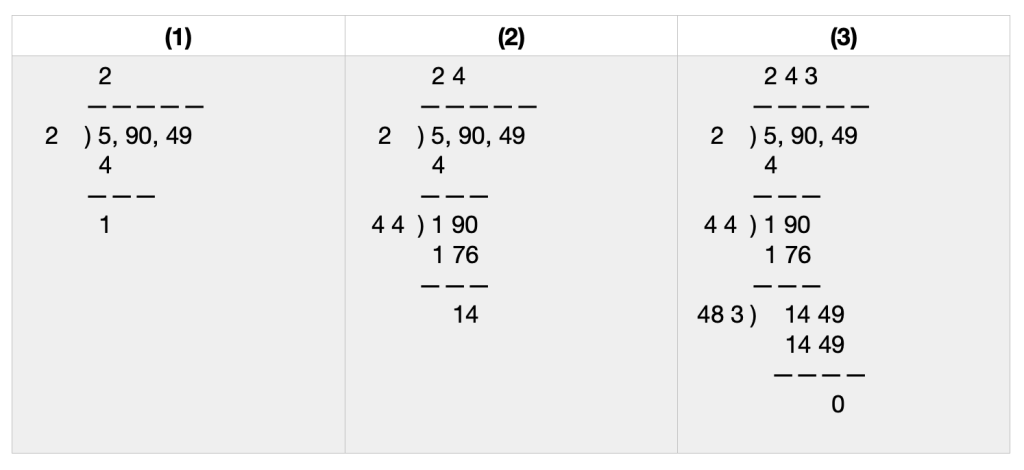
ஆக, 59049-ன் வர்கமூலம் 243.
இதனைக் காணொளியாக்கித் தந்துள்ளேன். பாருங்கள்.
இந்த வழிமுறையைப் பள்ளிக்கூடத்தில் சொல்லித் தருவதற்கு ஆசிரியர்கள் சிரமப்படுவார்கள், கற்றுக்கொள்ள மாணவர்களும் திண்டாடுவார்கள். இந்த வழிமுறையைத்தான் மாணவர்கள் முதலில் மறந்துபோகவும் செய்வார்கள். காரணம், ஏன் இதனைச் செய்கிறோம் என்பதில் தெளிவில்லாமல் இந்த வழிமுறை இருக்கிறது. ஆனால் ஆர்யபடர் சொல்லித்தரும் முறை மேலே உள்ளதிலிருந்து வேறுபட்டது. அதனைப் பார்ப்போம்.
இயற்கணிதத்தில் (அல்ஜீப்ராவில்) ஈருறுப்பு விரிவாக்கம் (Binomial expansion) என்பதை நீங்கள் படித்திருக்கலாம். (a+b)^n இதில் n என்பது 2, 3, 4 என்று ஏதேனும் முழு எண்ணாக இருக்கலாம். இதில் n=2 என்பதை எடுத்துக்கொள்வோம். (a+b)^2 = a^2 + 2ab + b^2
இதனை மனத்தில் வைத்துக்கொண்டால், ஆர்யபடரின் வழிமுறை புரிந்துவிடும். அவரும் கொடுத்துள்ள எண்ணை, வலமிருந்து இடமாக, இரண்டு இரண்டாகப் பிரித்துக்கொள்கிறார். விளைவாக, இடக்கோடி எண் ஒரு அல்லது இரண்டு இலக்கம் கொண்டதாக இருக்கும். இங்கும் முதலில் இடக்கோடி எண்ணுக்குள் பொருந்தக்கூடிய வர்க எண்ணைக் கண்டறியவேண்டும். முந்தைய எடுத்துக்காட்டான 4489 என்பதை எடுத்துக்கொள்வோம். 44-ல் அடங்குவது 6-ன் வர்கம். 44-ல் 36-க் கழித்தால் மீதம் 8.
ஆனால் இதற்கு அடுத்து, வழிமுறையில் மாற்றம் உருவாகிறது. a=6 என்று எடுத்துக்கொள்ளுங்கள். கொடுக்கப்பட்டுள்ள எண்ணில் a2-க் கழித்தாயிற்று. இப்போது மேலிருந்து, அடுத்து இருக்கும் இரண்டு எண்களில் முதலாவது எண்ணை மட்டும் கீழே கொண்டுவாருங்கள். b என்பதனை ஊகியுங்கள். ஊகித்து 2ab என்பதனைக் கழியுங்கள். மேலிருந்து அடுத்த எண்ணையும் கீழே கொண்டுவாருங்கள். அதில் b2 என்பதைக் கழியுங்கள்.
இதே முறையை மீண்டும் மீண்டும் தொடருங்கள். கீழே உள்ள செய்முறையைக் காணுங்கள்.

சரி, 59049 என்பதை எடுத்துக்கொண்டால்?

இதனைக் காணொளியாகப் பார்த்தால் மேலும் தெளிவாகப் புரியும்.
இதில் என்ன சிறப்பு? இதில் நாம் ஏன் நேரத்தைச் செலவிடவேண்டும்? இதனை அடுத்த பதிவில் பார்ப்போம்.
(தொடரும்)


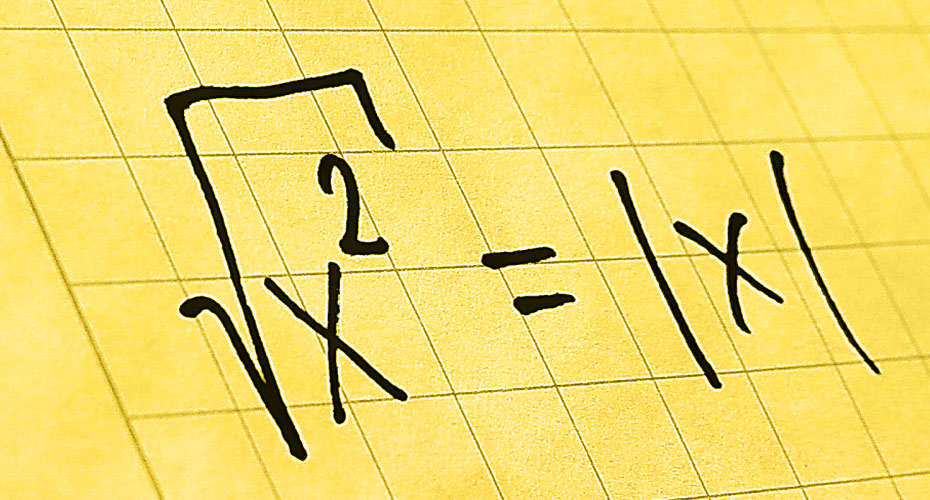
Well explained. This write will refered to all the school teachers, and research students. As simple as explained.
Our pranams
Wow… ❤️❤️
Interesting…
Sir, Super sir.. Child hood memories.. and this is ultimate… Jai Aryabhatar..
Wonderful writing sir. The article was very clear and neat. Far before i have been think about alternating ways to find Square root. through this article i have succeeded in my search. thank you so much
ஆரியபடர் குறித்தும் அவரது கணித முறைகள் பற்றியும் விரிவாக அனைத்துத் தரப்பினருக்கும் புரியும் வண்ணம் எளிமையாக விளக்கும் உங்கள் தொடருக்கு வாழ்த்துகள். மிகச் சிறப்பாக இருக்கிறது. அதேசமயம், உங்கள் காணொளியில் நீங்கள் எண்களைச் சுட்டுகையில், இதை, இங்கே, இதனோடு என்று சொல்வதற்குப் பதிலாக, எதை எதனோடு எங்கே என்பதைக் கொஞ்சம் அந்தந்த எண்களின் பெயர்களையே சொல்லி விளக்கினால், பார்வையற்ற மாணவர்களுக்கும் அது பயனுள்ளதாக அமையுமே. பரீசிலிக்குமாறு கேட்டுக்கொள்கிறேன்.
Comments are closed.